인공지능에서 게임은 상단히 좋은 연구주제 입니다.
Tic-Tac-Toe나 체스, 바둑과 같은 게임은 추상적으로 정의할 수 있고
지적 능력과 연관이 있는 것으로 생각되었습니다.
게임의 규칙을 아래와 같이 합니다.
1. 2인용 게임
2. 두 경기자를 MAX와 MIN으로 부름
3. 항상 MAX가 먼저 수를 둔다고 가정
4. 차례대로 수를 두는 게임만 대상으로 함(순차적인 게임)
5. 제로썸 게임- 한명이 승리하고 한명은 패배이며, 협동적인 승리는 없음
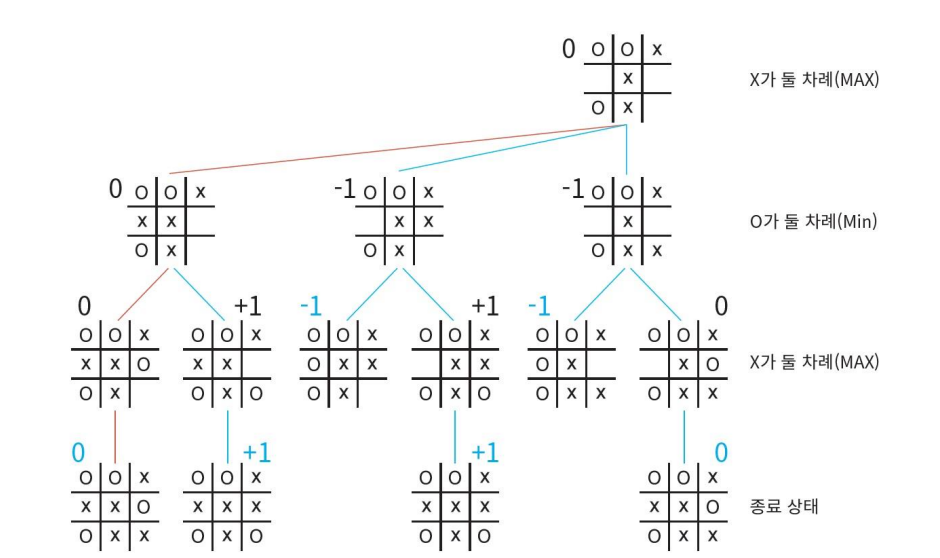
Tic-Tac-Toe 게임트리
Tic-Tac-Toe 게임트리의 일부입니다.

Tic-Tac-Toe 게임 트리의 크기는
게임보드가 3X3 크기를 가지고 있고, 한 곳에 수를 놓으면 다른 사람이 놓을 수 있는 곳이 하나 줄어들게 됩니다.
따라서 9*8*7*6*5*4*3*2*1 = 9! = 362,880이 됩니다.
그렇다면 362,880의 크기를 전부 계산할까요?
결론부터 이야기 하자면,
믈론 그런 경우도 존재할 수 있지만 그렇지 않을 때가 더 많습니다.
미니맥스(minimax) 알고리즘
미니맥스(minimax) 알고리즘에 대해 알아보겠습니다.

Tic-Tac-Toe를 해결하기 위한 Minimax 알고리즘을 실행할 때
보드의 모든 미래 가능한 상태를 시각화하여 작동하고 이를 트리 형태로 구성합니다.
현재 보드 상태가 알고리즘(트리의 루트)에 주어질 때,
'n' 가지(여기서 n은 AI에 의해 선택될 수 있는 이동의 수/AI가 될 수 있는 빈 셀의 수를 나타냄)로 분할됩니다.
이러한 새 상태 중 하나가 최종 상태인 경우 이 상태에 대해 더 이상 분할이 수행되지 않고
다음과 같은 방식으로 점수가 할당됩니다.
점수 = +1 (AI가 이기는 경우)
점수 = -1 (AI가 지는 경우)
점수= 0 (무승부가 발생하는 경우)
쉽게말해 상대방이 항상 최선의 수를 둔다는 가정하에, 보드의 다음 가능한 형태를 트리형태로 만들고 선택합니다.

MIN은 숫자가 작을 수록 이기고 MAX는 숫자가 클수 록 이길 확률이 높습니다.
따라서 아래에서부터 보면
MIN은 작은 숫자를 고르기 때문에 3과 2를 선택합니다.

MAX는 큰 수를 고르기 때문에 2와 3중 3을 선택합니다.
- 틱택토 게임에서의 미니맥스 예시 -
- 미니맥스 알고리즘 의사코드 -
function minimax(node, depth, maxPlayer)
if depth == 0 or node가 단말 노드 then
return node의 휴리스틱 값
if maxPlayer then
value ← −∞
for each child of node do
value ← max(value, minimax(child, depth − 1, FALSE))
return value
else // 최소화 노드
value ← +∞
for each child of node do
value ← min(value, minimax(child, depth − 1, TRUE))
return value
- 미니맥스 알고리즘의 시간 복잡도 -
매니맥스 알고리즘은 게임 트리에 대하여 완벽한 깊이 우선 탐색을 수행한다.
만약 트리의 최대 깊이가 m이고 각 노드에서의 가능한 수가 b개라면 최대최소 알고리즘의 알고리즘의 시간 복잡도는
O(𝑏^𝑚) 이다.
알파베타 가지치기
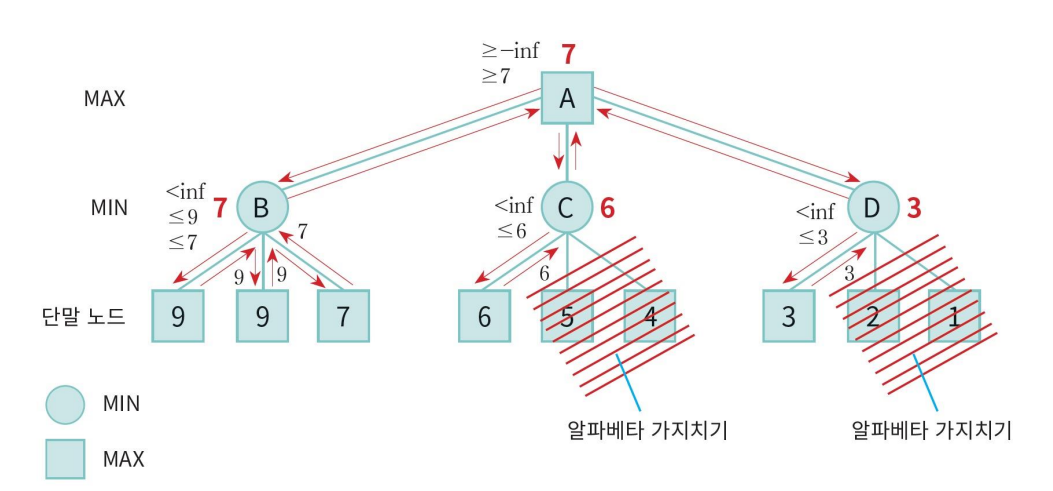
MINIMAX알고리즘에서 형성되는 탐색 트리 중에서 상당 부분은 결과에 영향을 주지 않으면서 가지들을 쳐낼 수 있다.
이것을 알파베타 가지치기라고 한다.
위 예시를 들어 설명하면 MAX는 -∞를 초기값으로, MIN은 +∞를 초기값으로 설정하고 노드를 탐색한다.
A -> B 로 갈 때 B는 초깃값 +∞ 와 9 중에서 MIN(+∞,9)를 하여 최소값 9를 찾는다.
이후 MIN(9,9) = 9 -> MIN(9,7) = 7 을 계산하여 최소값 7을 찾는다.
그리고 B의 단말 노드의 계산을 마친 후
A는 초기값 -∞ 와 B에서 찾은 최소값 7과 MAX(-∞, 7)을 계산하여 최대값 7을 찾는다.
여기서부터가 중요하다.
이제 A -> C 경로를 탐색하는데 이전 연산과 마찬가지로 MIN(+∞, 6) = 6 을 계산한다.
이후 C의 단말노드 5와 4는 계산해 볼 필요가 없다.
왜냐하면 A는 현재 가지고 있는 숫자 7보다 더 큰 숫자를 찾고 있는데 C는 6보다 작은 수를 찾아 보낼 것이기 때문이다.
A -> D 도 위와 같다.
따라서 부모의 현재 상태의 따라서 트리를 전부 탐색할 필요는 없다.
미니맥스 알고리즘에서 형성되는 탐색 트리 중에서 상당부분은 결과에 영향을 주지 않으면서 가지들을 쳐낼 수 있다.
이것을 알파베타 가지치기라고 한다.
탐색을 할 때 알파 값과 베타 값이 자식 노드로 전달된다.
자식 노드에서는 알파 값과 베타 값을 비교하여 불필요한 탐색을 중지할 수 있다.
MAX는 알파 값만을 업데이트하고 MIN은 베타 값만 업데이트 한다.
알파베타 알고리즘
function alphabeta(node, depth, a, b, maxPlayer)
if depth == 0 or node가 단말 노드 then
return node의 휴리스틱 값
if maxPlayer yhen //최대화 경기자
value ← -∞
for each child of node do
value ← max(value, alphabeta(child, depth-1, a, b, FALSE))
a ← max(a, value)
if a >= b then
break // 이것이 b 컷임.
//현재 노드의 최대 값이 부모 노드의 값(b)보다 커지게 되면 더 이상 탐색할 필요가 없음.
retuen value
else //최소화 경기자
value ← +∞
for each child of node do
value ← min(value, alphabeta(child, depth-1, a, b, TRUE))
b ← min(b, value)
if a >= b then
break // 이것이 a 컷임.
//현재 노드의 최소 값이 부모 노드의 값(a)보다 작아지게 되면 더 이상 탐색할 필요가 없음.
return value
불완전한 결정
미니맥스 알고리즘은 탐색 공간 전체를 탐색하는 것을 가정한다.
하지만 실제로는 탐색공간의 크기가 무척 크기 때문에 그렇게 할 수 없다.
실제로는 적당한 시간 안에 다음 수를 결정해야하기 때문이다.
이때는 탐색을 끝내야 하는 시간에 도달하면 탐색을 중간하고
탐색 중인 상태에 대하여 휴리스틱 평가 함수(evaluation function)를 적용해야 한다.
즉 비단말 노드이지만 단말 노드에 도달한 것처럼 생각하는 것이다.
참고
https://towardsdatascience.com/lets-beat-games-using-a-bunch-of-code-part-1-tic-tac-toe-1543e981fec1
'인공지능' 카테고리의 다른 글
| [인공지능] 오류 역전파 알고리즘 핵심 요약 - 경사 강하법(gradient descent) (0) | 2021.09.30 |
|---|---|
| [인공지능] 탐색 알고리즘 - 상태공간, 8-PUZZLE, 깊이 우선 탐색(DFS), 너비우선 탐색(BFS), 언덕 등반 기법, A* 알고리즘 (6) | 2021.09.14 |
| [인공지능] 파이토치(PyTorch)란? 설치방법 간략하게 소개 (0) | 2021.09.09 |
| [인공지능] 딥러닝이란? - 헷갈리는 의미와 학습 방법 3가지 쉽게 설명! (0) | 2021.09.09 |
| [인공지능] 인공지능의 겨울과 붐, 발전과 도약 (0) | 2021.09.06 |




댓글