초기 인공지능 학자들은 답을 찾는다라는 것에 집중하였는데,
그렇기 위해서는 탐색 기법을 잘 만들어야 한다고 생각했다고 한다.
우리가 잘 아는 알파고 또한 딥러닝과 탐색 기법을 통해 수를 읽었다.
탐색(search)이란 '상태공간에서 시작 상태->목표 상태까지의 경로를 찾는 것'
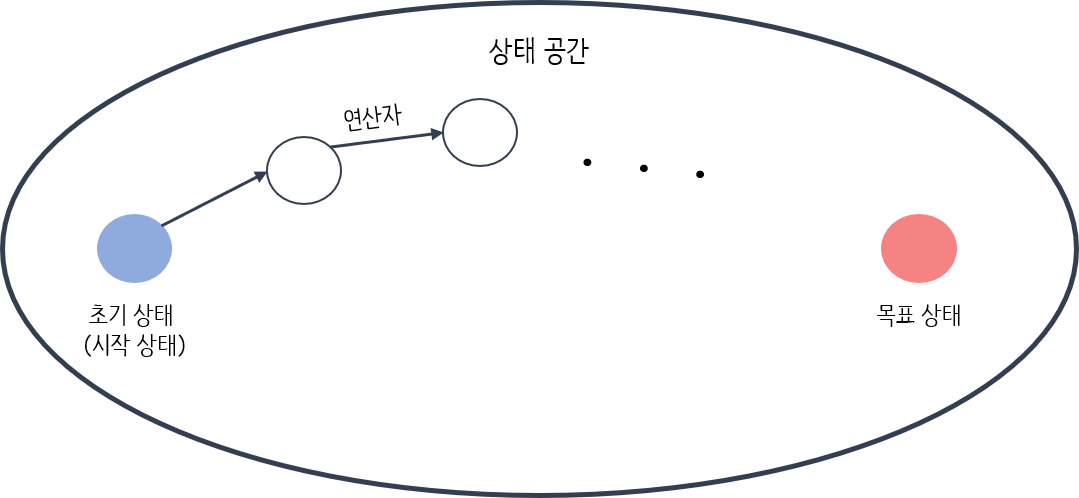
상태공간
*
상태공간(state space): 상태들이 모여 있는 공간
연산자: 다음 상태를 생성하는 것
시작상태: 초기상태
목표상태: 문제가 해결된 상태
8-PUZZLE
8-PUZZLE은 퍼즐을 최소한으로 이동하여 원래 상태로 맞추는 것이다.
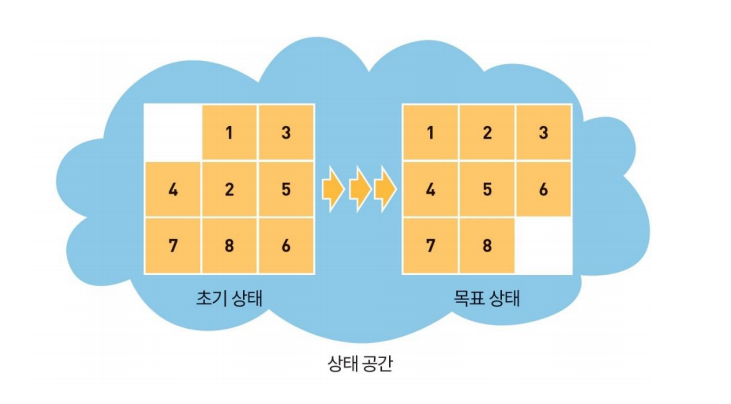
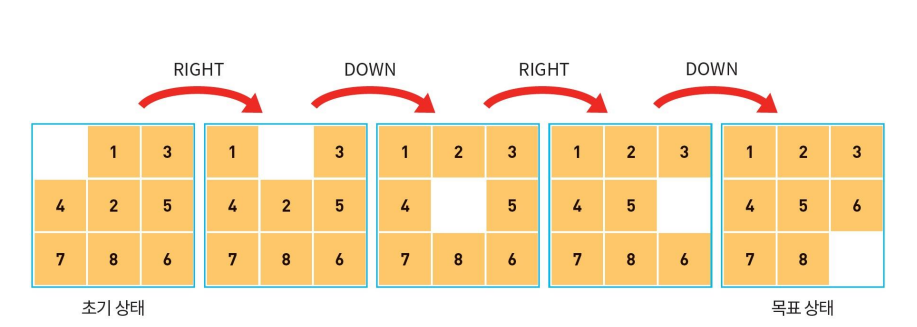
8-puzzle에서 연산자는 up, left, down, right 연산자로 4가지 연산이 가능.
(빈칸을 움직이는 것이 연산)
탐색 트리를 8-puzzle로 설명하면
상태 = 노드(node)
초기 상태 = 루트 노드
연산자 = 간선(edge)
이고,
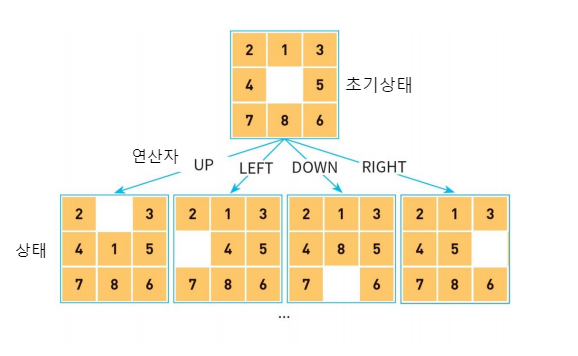
연산자를 적용하기 전까지 탐색트리는 미리 만들어져 있지 않으며
탐색 트리의 노드는 동적으로 생성 됩니다.
탐색 알고리즘
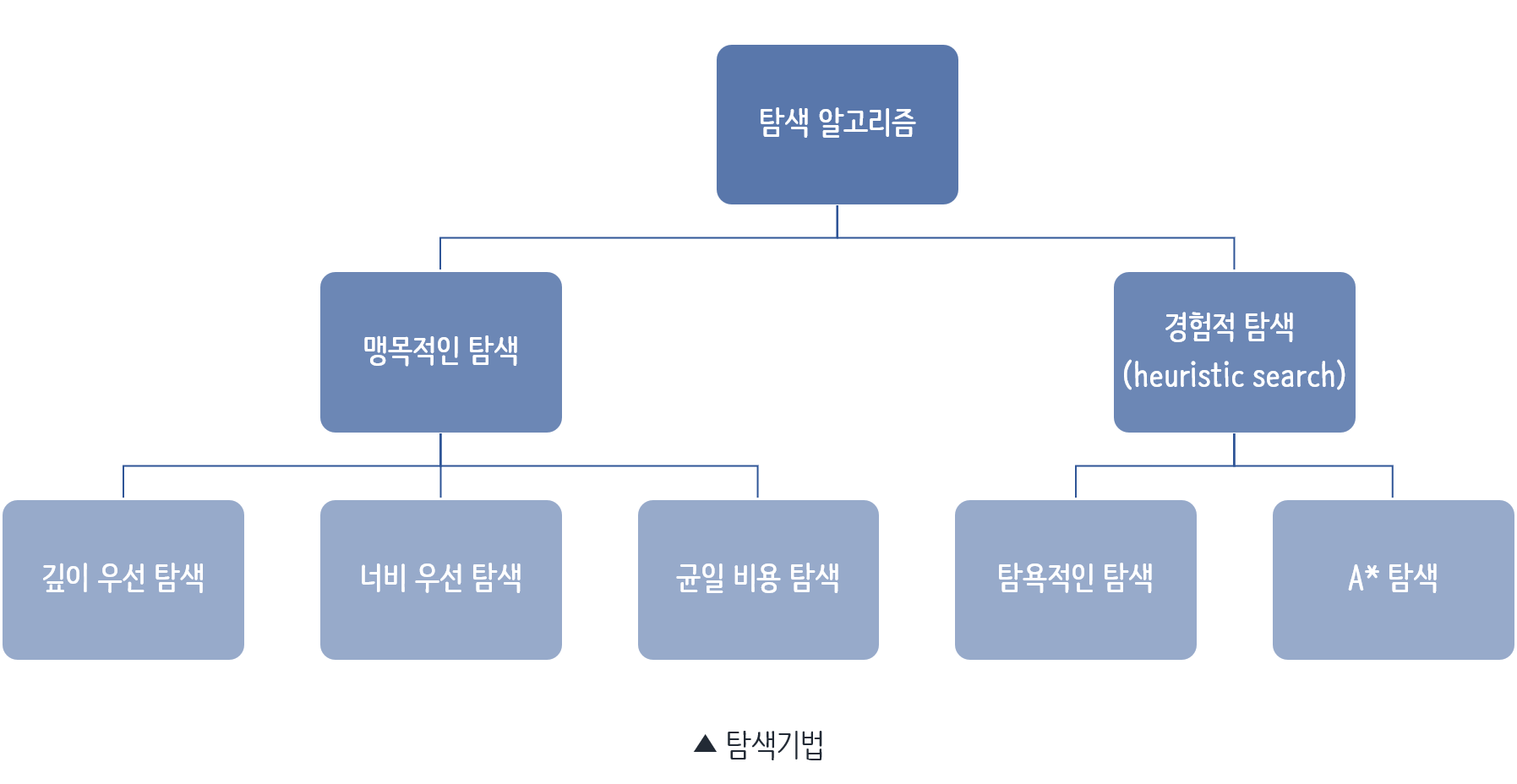
기본적인 탐색 기법의 종류 입니다.
이 중 깊이 우선 탐색과 너비 우선 탐색, A*알고리즘에 대해 소개하겠습니다.
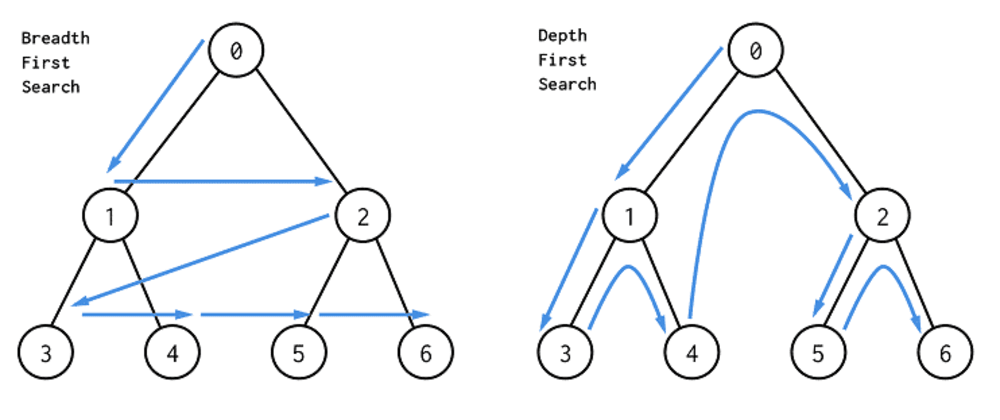
깊이 우선 탐색(Depth-First Search)은
탐색 트리 상에서 해가 존재할 가능성이 존재하는 한 앞으로 계속 전진하여 탐색하는 방법이고
너비 우선 탐색(Breadth-First Search)은
루트 노드의 모든 자식 노드들을 탐색한 후에 해가 발견되지 않으면 한 레벨 내려가서
동일한 방법으로 탐색을 계속하는 방법 입니다.
탐색 에서는 중복된 상태를 막기 위해 OPEN 리스트와 CLOSED 리스트를 사용합니다
OPEN 리스트는 확장은 되었으나 아직 탐색하지 않은 상태들이 들어 있는 리스트이고,
CLOSED 리스트는 탐색이 끝난 상태들이 들어 있는 리스트 입니다.
예를 들어보겠습니다.
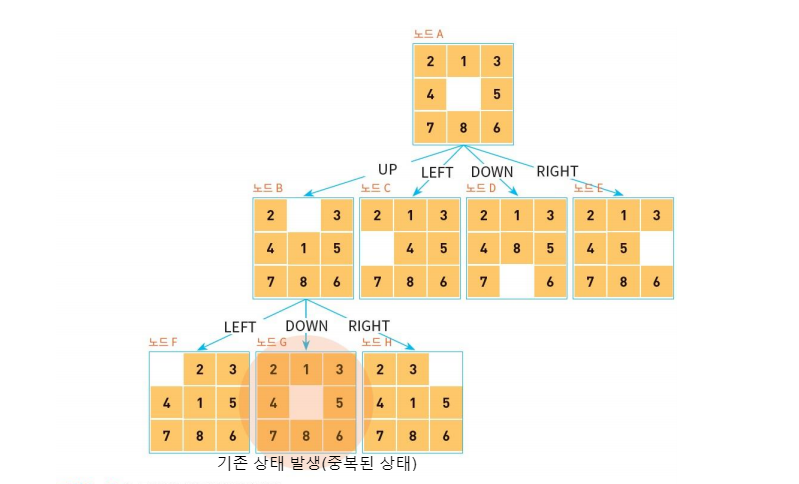
깊이 우선 탐색에서 확장을 하던 도중 중복된 상태가 발생합니다.
그럴 때 OPEN 리스트와 CLOSE 리스트에 들어있는 상태와 비교하여 리스트에 들어 있는 상태는 생성하지 않습니다.
깊이 우선 탐색(DFS) 알고리즘
//의사코드 depth_first_seatch() open <- [시작노드] //확장은 됐지만 탐색은 ㄴㄴ closed <- [] while open ≠ [] do //확장된 상태가 있으면 계속 실행 X <- open 리스트의 첫번째 요소 if X == goal then return SUCCESS //목표 상태 도달 else X의 자식 노드를 생성한다. X를 closed 리스트에 추가한다. X의 자식 노드가 이미 open이나 closed에 있다면 버린다. 남은 자식 노드들은 open의 처음에 추가한다.(스택처럼 사용) LIFO return FAIL
너비 우선 탐색(BFS) 알고리즘
//의사코드 depth_first_seatch() open <- [시작노드] //확장은 됐지만 탐색은 ㄴㄴ closed <- [] while open ≠ [] do //확장된 상태가 있으면 계속 실행 X <- open 리스트의 첫번째 요소 if X == goal then return SUCCESS //목표 상태 도달 else X의 자식 노드를 생성한다. X를 closed 리스트에 추가한다. X의 자식 노드가 이미 open이나 closed에 있다면 버린다. 남은 자식 노드들은 open의 끝에 추가한다.(큐처럼 사용) FIFO return FAIL
깊이 우선 탐색과 너비 우선 탐색은 맹목적이게 목표를 찾기 때문에 비 효울적이라고 볼 수 있습니다.
그리고 목표가 어디에 있는지에 따라 극단적인 상황이 나올 수 있습니다.
만약 우리가 문제 영역에 대한 정보나 지식을 사용할 수 있다면 탐색 작업을 더 빠르게 할 수 있습니다.
이것을 경험적 탐색 방법(Heuristic Search Method) 또는 휴리스틱 탐색 방법이라고 부릅니다.
그리고 이때 사용되는 정보를 휴리스틱 정보(Heuristic infomation)라고 합니다.
8-puzzle에서의 휴리스틱
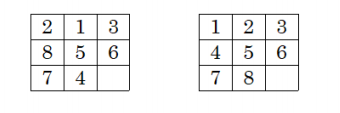
만약 현재 상태와 목표 상태가 다음과 같다고 가정 할 때 [3, 5, 6, 7]은 목표상태와 같습니다.
h1(N) = 현재 제 위치에 있지 않은 타일의 개수 = 1+1+1+1=4
(h1(N) = 0 목표 상태, 작을 수 록 좋음)
h2(N) = 각 타일의 목표 위치까지의 거리 = 1+1+0+2+0+0+0+2=6
ex) 2가 1의 위치로 가기 위해서는 한칸 움직여야 함.
(h2(N) = 0 목표 상태, 작을 수 록 좋음)
언덕 등반 기법
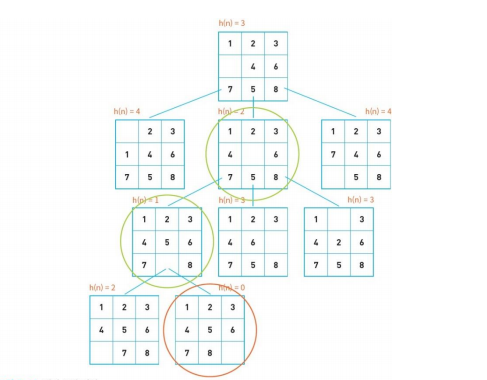
언덕 등반 기법은 평가 함수의 값이 좋은 노드를 먼저 처리한다.
평가함수로 제 위치에 있지 않은 타일의 개수를 사용.
경험적인 탐색 방법은 무조건 휴리스틱 함수 값이 가장 좋은 노드만을 선택한다.
이건 등산할 때 무조건 현재의 위치보다 높은 위치로만 이동하는 것과 같음.
일반적으로는 현재의 위치보다 높은 위치로 이동하면 산의 정상에 도달할 수 있음.
언덕 등반 기법 알고리즘
1. 먼저 현재 위치를 기준으로 해서, 각 방향의 높이를 판단(노드의 확장)
2. 만일 모든 위치가 현 위치보다 낮다면 그 곳을 정상이라고 판단(목표 상태인지 점검)
3. 현 위치가 정상이 아니라면 확인 된 위치 중 가장 높은 곳으로 이동(후계노드의 선택)
지역 최소 문제
순수한 언덕 등반 기법은 오직 h(n) 값만을 사용한다.
(open 리스트나 closed 리스트도 사용 안함)
이런 경우에는 생선된 자식 노드의 평가함수 값이 부모 노드보다 더 높거나 같은 경우가 나올 수 있다.
이것을 지역 최소 문제(local minima problem)라고 한다.
A* 알고리즘
A* 알고리즘은 평가 함수의 값을 다음과 같은 수식으로 정의한다.
f(n) = g(n) + h(n)
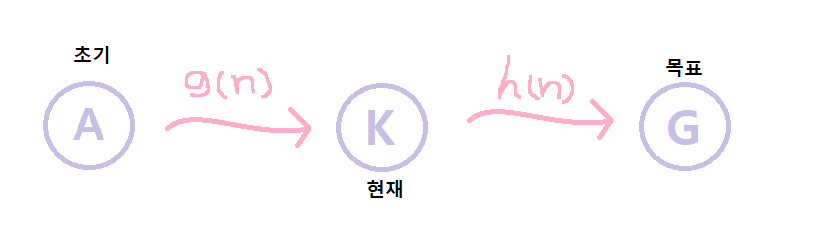
g(n): 시작 노드에서 현재 노드까지의 비용
h(n): 현재 노드에서 목표 노드까지의 거리
8-puzzle 에서의 A* 알고리즘
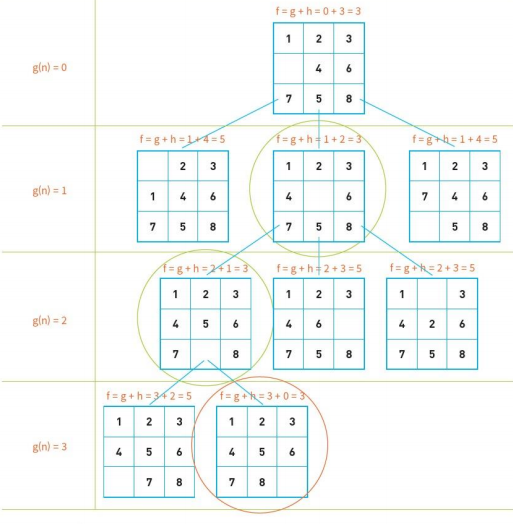
AStar_search() open <- [시작노드] closed <- [] while open ≠ [] do X <- open 리스트에서 가장 평가 함수의 값이 좋은 노드 if X == goal then return SUCCESS else X의 자식 노드를 생성 X를 closed 리스트에 추가 if X의 자식 노드가 open이나 closed에 있지 않으면 자식 노드의 평가 함수 값 f(n) = g(n) + h(n)을 계산 자식 노드들을 open에 추가 return FAIL
TSP
TSP(Travelling Salesman Problem)은 "도시의 목록과 도시들 사이의 거리가 주어졌을 때,
하나의 도시체서 출발하여 각 도시를 방문하는 최단의 경로는 무엇인가?"이다.
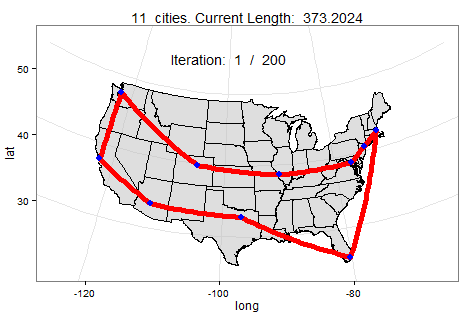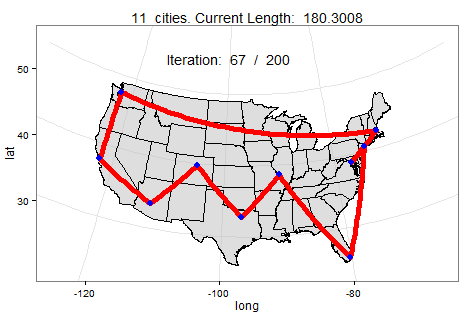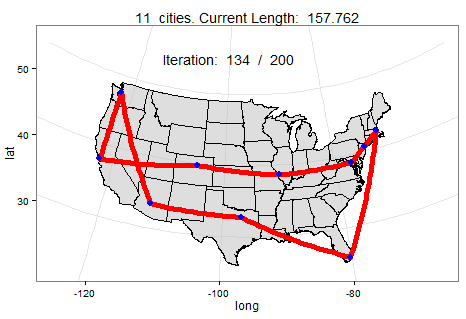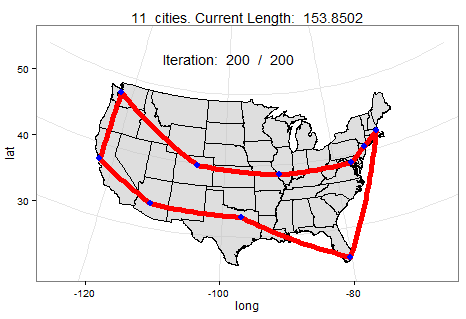
이것은 최적화 문제에서 중요한 문제이며 각 도시의 거리, 시간, 비용 등을 전부 계산하여 최고의 방법을 찾아야한다.
'인공지능' 카테고리의 다른 글
| [인공지능] 게임 트리 - 미니맥스(minimax) 알고리즘, 알파베타 가지치기, 휴리스틱 평가 함수(evaluation function) (0) | 2021.11.14 |
|---|---|
| [인공지능] 오류 역전파 알고리즘 핵심 요약 - 경사 강하법(gradient descent) (0) | 2021.09.30 |
| [인공지능] 파이토치(PyTorch)란? 설치방법 간략하게 소개 (0) | 2021.09.09 |
| [인공지능] 딥러닝이란? - 헷갈리는 의미와 학습 방법 3가지 쉽게 설명! (0) | 2021.09.09 |
| [인공지능] 인공지능의 겨울과 붐, 발전과 도약 (0) | 2021.09.06 |




댓글